Informed by our analysis throughout the semester, we will build our final model to predict the winner of the 2024 US presidential election.
Origins
Our model is inspired by the simple and powerful Abramowitz model below.
\[ \underbrace{\text{pv2p}}_{\text{incumbent party}} = \beta_0 + \beta_1 \cdot \underbrace{\text{G2GDP}}_{\text{Q2 GDP growth}} + \beta_2 \cdot \underbrace{\text{NETAPP}}_{\text{June Gallup job approval}} + \beta_3 \cdot \underbrace{\text{TERM1INC}}_{\text{sitting pres}} \]
To compare it with our final model, which uses data limited to 2008 onward, let’s find its performance on elections since 2008.
## Abramowitz LOO-CV RMSE: 3.57## Abramowitz LOO-CV prediction error: 5.76 %Instead of the popular vote, let’s build upon the model to predict the 2024 winner of the electoral college.
We will use this metric to evaluate our model: leave-one-out root mean square error (LOO-RMSE) of competitive states.
Modifications
Moving from national to state-level
To predict the winner of the electoral college we need to predict the two-party vote share of each state. We will replace the Q2 GDP growth variable from national to state-level, and the June Gallup job approval to state-level presidential polls 20 weeks before the election.
## State-level Abramowitz LOO-CV RMSE: 2.7## State-level Abramowitz LOO-CV RMSE (swing-states): 1.87It seems like the LOO-CV for non-swing states is dragging up the error. Let’s try to reduce it by incorporating by sets swing states and non-swing states apart: political calcification.
Political calcification
Let’s incorporate past voting records into the prediction.
## State-level Abramowitz LOO-CV RMSE: 2.18## State-level Abramowitz LOO-CV RMSE (swing-states): 1.55This gives our final model \[ \text{pv2p} = \beta_0 + \beta_1 \cdot \text{G2GDP} + \beta_2 \cdot \text{NETAPP} + \beta_3 \cdot \text{TERM1INC} + \beta_4 \cdot \text{LAG} \]
Where:
| Variable | Explanation |
|---|---|
| \(\text{pv2p}\) | State-level incumbent party pv2p |
| \(\text{G2GDP}\) | State-level Q2 GDP growth |
| \(\text{NETAPP}\) | State-level two-candidate poll |
| \(\text{TERM1INC}\) | Sitting president? |
| \(\text{LAG}\) | State-level previous election pv2p |
Prediction
We predict the Democratic two-party vote share for states that we have accurate data. This includes all toss up and lean states.
## inc_poll2p q2_gdp_growth incumbent inc_lag swing state preds
## 1 37.67027 4.8 FALSE 39.30639 0 Utah 34.70161
## 2 40.27197 3.2 FALSE 41.60282 0 Montana 37.63480
## 3 41.20502 5.3 FALSE 40.21595 0 Nebraska 37.71462
## 4 41.13118 2.8 FALSE 41.80495 0 Indiana 38.41583
## 5 42.70967 3.9 FALSE 42.16418 0 Missouri 39.65488
## 6 43.60563 4.5 FALSE 44.07339 0 South Carolina 40.89483
## 7 45.50763 3.4 FALSE 45.92330 0 Ohio 43.08545
## 8 45.89562 2.8 FALSE 47.16928 0 Texas 43.84368
## 9 46.46802 3.2 FALSE 48.30525 0 Florida 44.60786
## 10 48.64684 3.1 FALSE 50.15683 1 Arizona 46.91211
## 11 49.34202 3.5 FALSE 49.31582 1 North Carolina 47.15368
## 12 49.23615 3.5 FALSE 50.11933 1 Georgia 47.32206
## 13 49.87216 3.2 FALSE 50.58921 1 Pennsylvania 48.00091
## 14 49.65457 1.8 FALSE 51.22312 1 Nevada 48.17480
## 15 50.40200 4.2 FALSE 50.31906 1 Wisconsin 48.22843
## 16 50.37702 4.2 FALSE 51.41356 1 Michigan 48.55158
## 17 52.47830 2.1 FALSE 53.74835 0 New Hampshire 51.15547
## 18 53.00349 1.3 FALSE 53.63951 0 Minnesota 51.61822
## 19 53.33396 3.2 FALSE 55.15469 0 Virginia 52.15390
## 20 53.51912 1.7 FALSE 55.51849 0 New Mexico 52.57045
## 21 55.84436 2.7 FALSE 56.93832 0 Colorado 54.73955
## 22 58.68588 3.8 FALSE 61.71683 0 New York 58.35623
## 23 60.25346 2.2 FALSE 59.92550 0 Washington 59.19569
## 24 62.80274 2.8 FALSE 64.90891 0 California 62.69898
## 25 64.25257 1.9 FALSE 67.11555 0 Massachusetts 64.62473
## 26 64.77992 2.3 FALSE 67.02905 0 Maryland 64.97059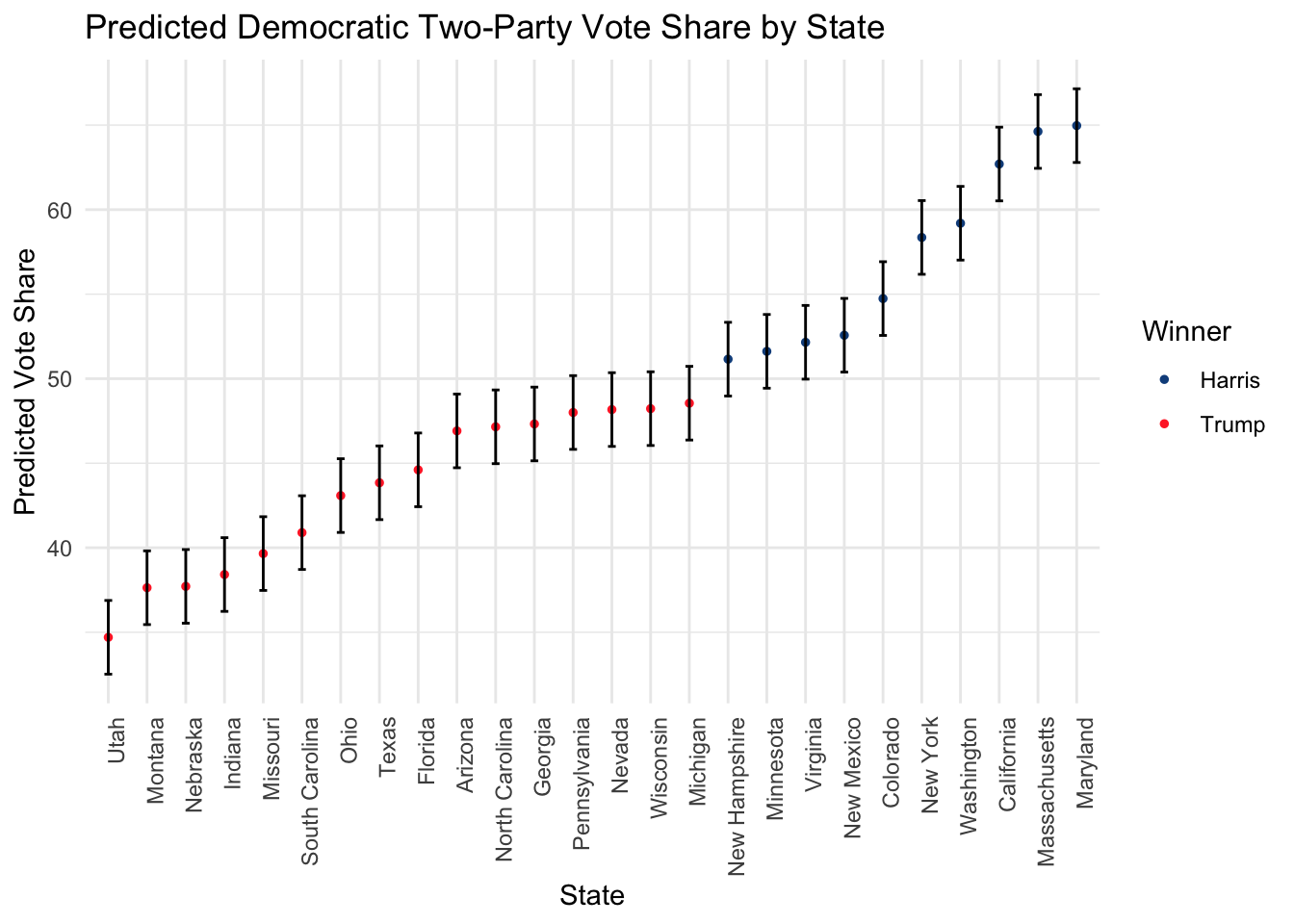
For the rest of the states, which are solid or likely states according to Cook’s Political Report, we will assign it assuming that the expert predictions are correct.
 Trump wins with 312 against Harris’ 226
Trump wins with 312 against Harris’ 226
Uncertainty
Here we simulate 10,000 possible cases. Here we plotted the uncertainty for the states assuming that the errors are independent. Regardless of whether the errors are correlated across states, marginally the plots will look the same.
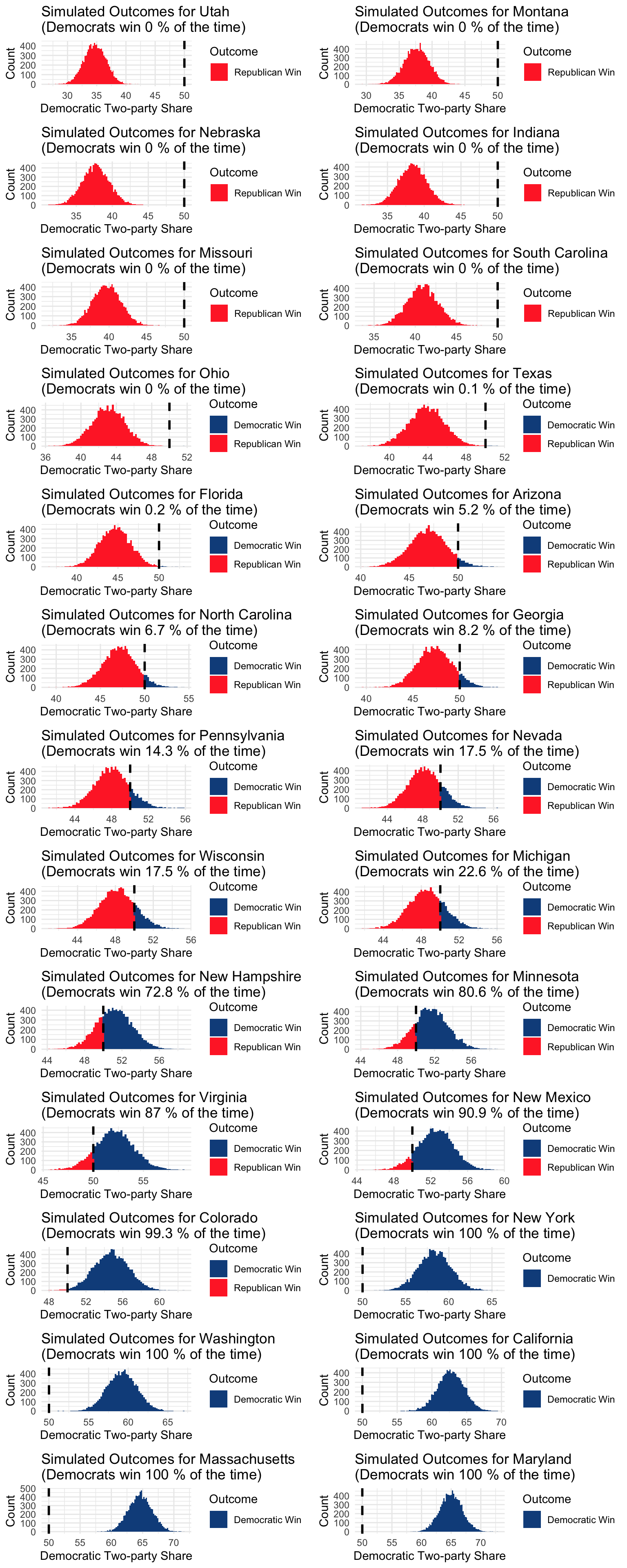
How about the electoral college?
Here for each simulation we assume that the states share the same error.
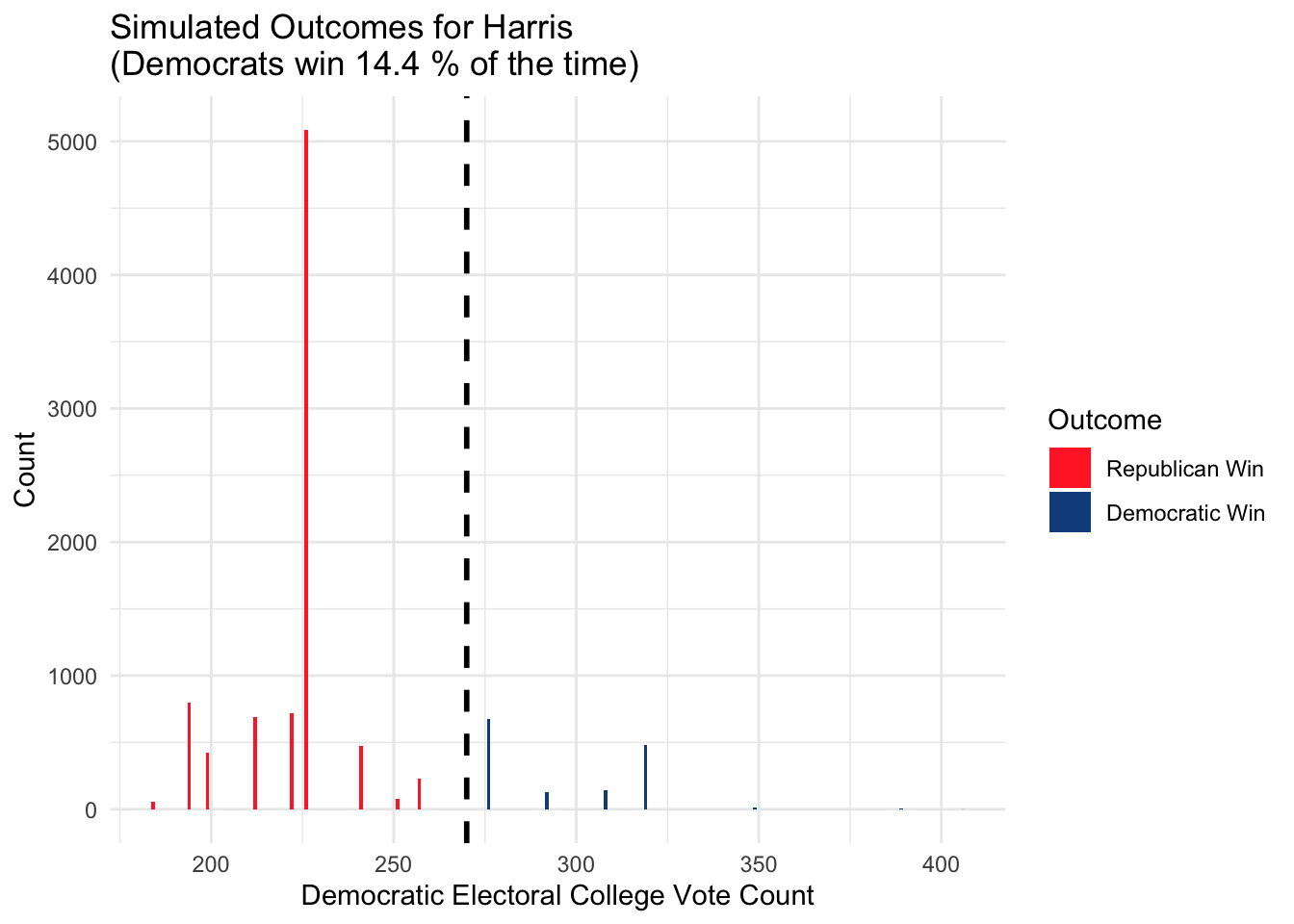
If we instead assume that states have independent error (which I think is less reasonable than all states sharing the same error), we will have a <2% chance of a Democrat win.
Updated on 4 Nov to include latest polls.
Appendix
Here are other ideas that didn’t improve the model.
A later economy
Instead of Q2 GDP growth, Q3 GDP growth comparison is closer to the election.
## State-level Abramowitz LOO-CV RMSE: 2.28## State-level Abramowitz LOO-CV RMSE (swing-states): 1.69Partisanship
Voters might vote along partisan lines. Let’s incorporate the party where the incumbent candidate is from.
## State-level Abramowitz LOO-CV RMSE: 2.13## State-level Abramowitz LOO-CV RMSE (swing-states): 1.59A longer horizon for the economy
How about using a GDP growth compared to 3 years ago?
## State-level Abramowitz LOO-CV RMSE: 2.18## State-level Abramowitz LOO-CV RMSE (swing-states): 1.64More sophisticated models
Let’s see if using a random forest helps.
## State-level Abramowitz LOO-CV RMSE: 3.05## State-level Abramowitz LOO-CV RMSE (swing-states): 2.65Swing state behavior
Swing states might have inherently different dynamics than other states. For example, they are the battleground states where campaign spending are being focused on. Let’s add a flag on whether a state is consider a swing state in that election.
## State-level Abramowitz LOO-CV RMSE: 2.19## State-level Abramowitz LOO-CV RMSE (swing-states): 1.53National GDP
Some literature suggests that using national-level GDP is more accurate than using state-level GDP.
## State-level Abramowitz LOO-CV RMSE: 12.61## State-level Abramowitz LOO-CV RMSE (swing-states): 12.36